Brent T. Morgan
About
Research: Academic
Distributed Computing, MPI
ML Optimization, SP-GOPT
Thomson Problem, Solutions
Research: Games
Quant Trading
Blackjack
Sports Betting
Rubik's Cube Algorithms
Software
SP-GOPT Solver

Sports Betting/Wagering/Gambling

 

Me and Bill Benter, 2017. Mr. Benter, originally a physics student, became a card counter of blackjack and later, went on to focus on sports betting using statistical, mathematical, techniques. I met him at the Blackjack Ball in 2017.

Objective

For any sports market, a generalizable framework is as follows. For a payout odds of implied probability \(p_{\text{market}}\), by using a set of historical features and signals of truth, \(\vec{X}_{\text{training}}\), \(y_{\text{training, truth}}\), model \(M\) and modeling parameters \(\vec{A}\), then the objective is to try to minimize a cost function \(C\left(M\left(\vec{A}, \vec{X}_{\text{training}}\right),y_{\text{training, truth}}\right)\) to arrive at an optimal set of parameters, \(\vec{A}^{*}\),

\[ \begin{equation} \vec{A}^{*} = \underset{\vec{A}}{\text{argmin }} C\left(M\left(\vec{A},\vec{X}_{\text{training}}\right),y_{\text{training, truth}}\right)\label{eq:1} \end{equation} \]

and thus, try to ensure \(M\left(\vec{A}^{*},\vec{X}_{\text{test}}\right) = p_{\text{predict}} > p_{\text{market}}\) where \(y_{\text{test, truth}}=1\). Additionally, to maximize wagering effectiveness, optimal wagers \(\vec{W}^{*}\) are found with an expectation maximization for the expected payout \(E\left[P_{\text{payout}}\left(\tilde{p}_{\text{market}}, \vec{W}\right)\right]\), for wagers \(\vec{W}\), where \(\tilde{p}_{\text{market}}=\tilde{p}_{\text{market}}\left(p_{\text{predict}}\right)\) is the predicted \(p_{\text{market}}\):

\[ \begin{equation} \vec{W}^{*} = \underset{\vec{W}}{\text{argmax }} E\left[P_{\text{payout}}\left(\tilde{p}_{\text{market}}, \vec{W}\right)\right].\label{eq:2} \end{equation} \]

Thus, a prediction and wagering strategy results in maximizing overall expectated return; using \(\eqref{eq:1}\) and \(\eqref{eq:2}\), across \(n\) wagering opportunities,

\[ \text{Expected return} = \displaystyle\sum_{i}^{n} p_{\text{predict}}\left(\vec{A}^{*},\vec{X}_{\text{test}}\right)_{i}E\left[P_{\text{payout}}\left(\tilde{p}_{\text{market}}, \vec{W}\right)\right]_{i}. \; \llap{\mathrel{\boxed{\phantom{\text{Expected return} = \displaystyle\sum_{i}^{n} \tilde{p}_{\text{predict}}\left(\vec{A}^{*},\vec{X}_{\text{test}}\right)_{i}E\left[P_{\text{payout}}\left(p_{\text{market}}, \vec{W}\right)\right]_{i}…}}}} \]

\[ \text{Realized return} = \displaystyle\sum_{i}^{n} y_{\text{test, truth}, i}P_{\text{payout}}\left(p_{\text{market}}, \vec{W}\right)_{i}. \; \llap{\mathrel{\boxed{\phantom{\text{Realized return} = \displaystyle\sum_{i}^{n} y_{\text{test, truth},i}P_{\text{payout}}\left(p_{\text{market}}, \vec{W}\right)_{i}…}}}} \]

We end up having to use numerical optimization techniques and high performance computing to solve such functions, where the objective functions are tailored to the sport of interest. This is generalizable to any (non-sports) market, as well.

Results

I have personal experience in systematically / algorithmically wagering on a sport, using techniques from domains of mathematical modeling, Data Science, computation, numerical optimization, to result in the following revenue made:

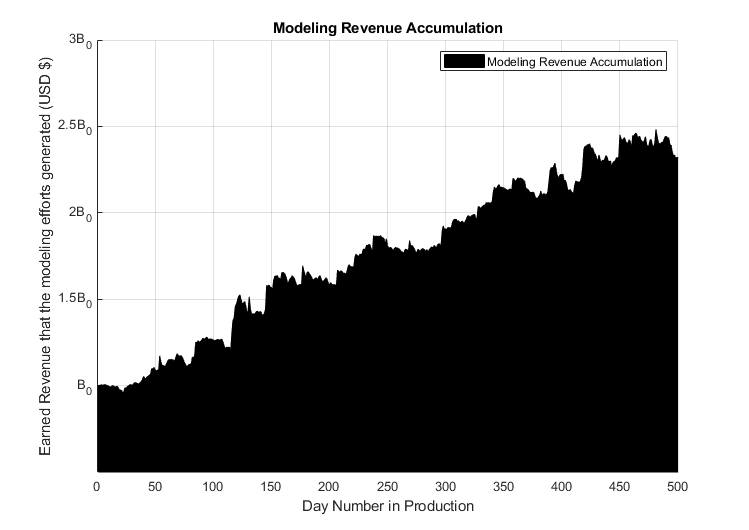\(B_{0}\) is initial bankroll of betting account, equal to an undisclosed amount. The above is revenue accumulation resulting from 500 days of models being implemented in a live production environment. This is a proof of concept that wagering on sports can (in the long run) systematically win. This is based on real daily updated reports from a betting exchange; results are verifiable.


This also confirms Bill Benter's claims that successful algorithmic sports wagering can be a profitable endeavor.

References